VITS 论文阅读-2

方法

所提出的方法主要在前三小节中描述：

• 条件VAE公式（a conditional VAE formulation）
• 基于变分推理的对准估计（alignment estimation derived from variational inference）
• 提高合成质量的对抗性训练（adversarial training for improving synthesis quality）

图1a和1b分别显示了我们方法的训练和推理过程。从现在起，我们将把我们的方法称为端到端文本到语音（VITS），具有对抗性学习的变分推理。

训练和推理流程如下：

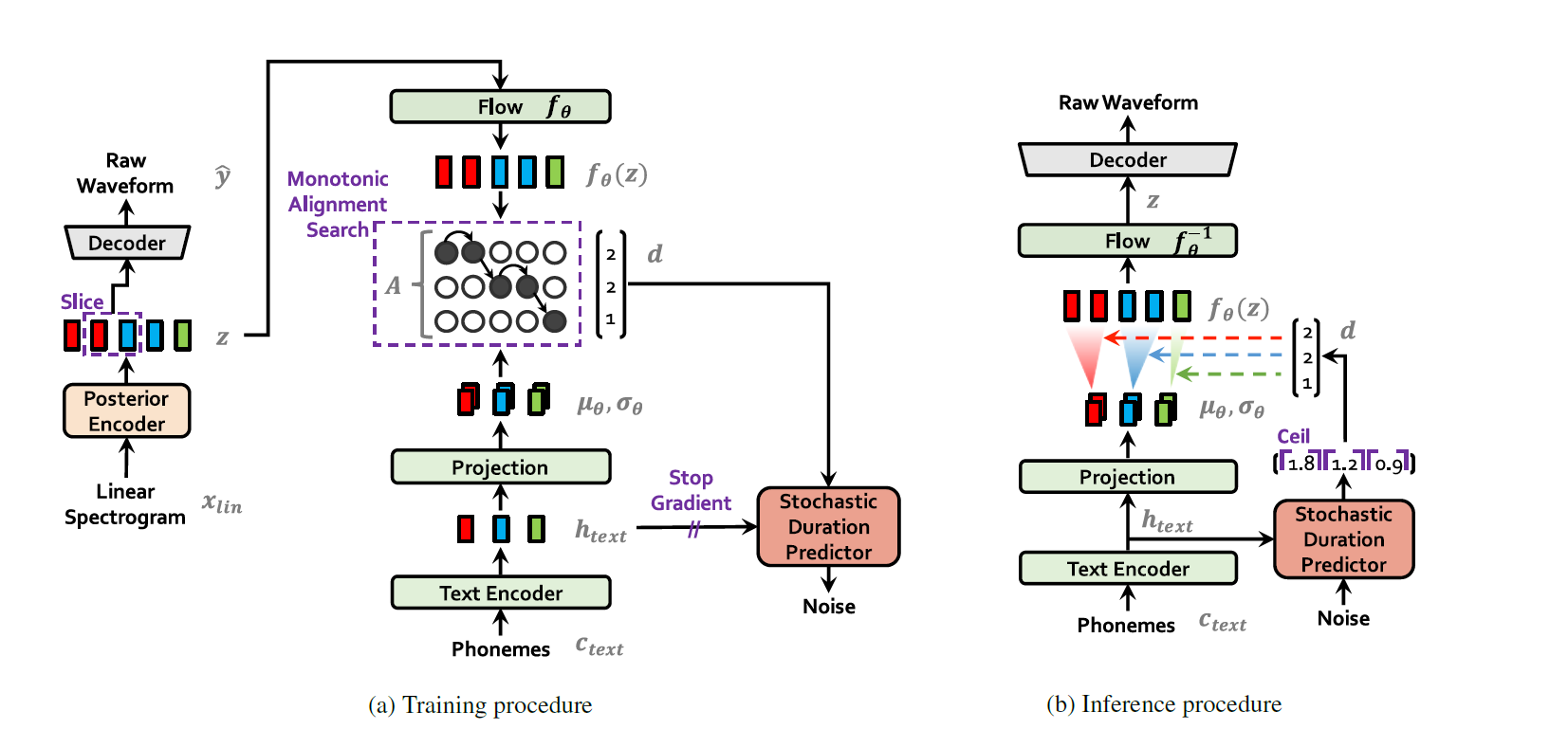
条件推理（conditional inference）

条件VAE公式（a conditional VAE formulation）。

目标为一个”变分下界”，也叫证据下界（ELBO）。详细说就是“intractable marginal log-likelihood ”棘手边缘拟合对数似然的变分下界。

如图，$\log p{\theta}(x \mid c)$的变分下界为$\mathbb{E}{q{\phi}(z \mid x)}\left[\log p{\theta}(x \mid z)-\log \frac{q{\phi}(z \mid x)}{p{\theta}(z \mid c)}\right]$。

$$L_{\text {recon }}=\left\|x_{mel}-\hat{x}_{mel}\right\|_{1}$$

下界：似然【数据点x的似然函数 - （近似后验分布 / 条件c下潜变量z的先验分布）的对数】

训练损失即负的ELBO。

也可以看作为重建损失 + KL散度，这在潜变量z服从近似后验分布时成立。

重建损失

作为重建损失中的目标数据点，我们使用mel频谱图而不是原始波形，由 $x{mel}$ 表示。我们通过解码器将潜在变量z上采样到波形域 $\hat{y}$ ，并将 $\hat{y}$ 变换到融合谱图域 $\hat{x}{mel}$ 。然后，预测的和目标mel谱图之间的L1损失被用作重建损失：

$$L_{\text {recon }}=\left\|x_{mel}-\hat{x}_{mel}\right\|_{1}$$

这可以被视为假设数据分布的拉普拉斯分布并忽略常数项的最大似然估计。我们定义了mel声谱图域中的重建损失，以通过使用近似人类听觉系统响应的mel标度来提高感知质量。注意，根据原始波形的mel谱图估计不需要可训练的参数，因为它只使用STFT和线性投影到mel标度上。此外，估计仅在训练期间使用，而不是推理。 在实践中，我们不对整个潜在变量z进行上采样，而是使用部分序列作为解码器的输入，这是用于高效端到端训练的窗口生成器训练。

KL收敛

先验编码器c的输入条件由从文本中提取的音素$c_{text}$和音素与潜在变量之间的对齐 A 组成。

对齐是一个硬单调注意力矩阵，其$\mid c_{text}\mid \times \mid z\mid$维度表示每个输入音素扩展到与目标语音时间对齐的长度。由于对齐没有基本事实标签，我们必须在每次训练迭代时估计对齐。

在我们的问题设置中，我们的目标是为后验编码器提供更多的高分辨率信息。因此，我们使用目标语音$x_{lin}$的线性尺度频谱图作为输入，而不是mel频谱图。注意，修改后的输入并不违反变分推理的性质。那么KL分歧是：

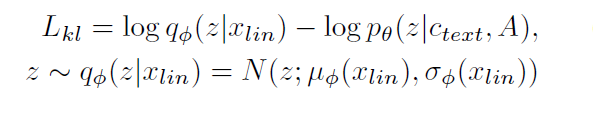
“因子分解正态分布”用于参数化我们的先验和后验编码器。

我们发现，增加先验分布的表现力对于生成真实样本很重要。因此，我们应用归一化流 f ，该流允许在因子分解的正态先验分布之上，根据变量变化规则，将简单分布可逆变换为更复杂的分布。

路线估计（Alignment Estimation）

基于变分推理的对准估计（alignment estimation derived from variational inference）。

单调对齐搜索（MONOTONIC ALIGNMENT SEARCH）

为了估计输入文本和目标语音之间的对齐A，我们采用单调对齐搜索（MAS）。

这是一种搜索对齐的方法，其最大化了由归一化流 f 参数化的数据的可能性。

因为人类按顺序阅读文本，不跳过任何单词，候选比对（ candidate alignments）被限制为单调且不跳过。

为了找到最佳对准，Kim等人（2020）使用动态规划。在我们的这个情况下直接应用MAS是困难的，因为我们的目标是ELBO，而不是确切的对数似然。因此，我们重新定义MAS，以找到最大化ELBO的对齐。

这个过程简化为找到最大化潜在变量z的对数似然的对齐。

但事实上，无论修不修改，都可以工作。因此我们使用的是原始MAS。

文本时长预测器（DURATION PREDICTION FROM TEXT）

我们可以通过对估计的对齐$\sum{j}^{} A{i,j}$的每行中的所有列求和来计算每个输入token$d_i$的持续时间。但持续时间可以用来训练确定性的持续时间预测器，但它不能表达一个人每次以不同的语速说话的方式。

为了生成类似人类的语音节奏，我们设计了一个随机持续时间预测器，使其样本遵循给定音素的持续时间分布。

随机持续时间预测器是一种基于流的生成模型，通常通过最大似然估计进行训练。然而，最大似然估计的直接应用是困难的，因为每个输入音素的持续时间是

1）离散整数，其需要被去量化（dequantized）以使用连续归一化流。

2）标量，其由于可逆性而无法进行高维变换。

我们应用变分去量化和变分数据扩充来解决这些问题。

具体地说，我们引入了两个随机变量 u 和 v ，它们具有与持续时间序列 d 相同的时间分辨率和维度，分别用于变分去方程化和变分数据扩充。

我们将u的支持度限制为[0, 1），使得差$d-v$变成了一个正实数序列。

我们按通道连接 v 和 d ，以生成更高维的潜在表示。、

我们通过近似后验分布$q(u,v|d,c{text})$对这两个变量进行采样。由此产生的目标是音素持续时间的对数似然的变分下界。训练损失$L{dur}$是负变分下界。

我们将阻止输入梯度反向传播的”停止梯度算子”应用于输入s，保证持续时间预测器的训练不会影响其他模块的训练。

而取样程序相对简单：通过随机持续时间预测器的逆变换，从随机噪声中采样音素持续时间，然后将其转换为整数。

对抗训练

提高合成质量的对抗性训练（ adversarial training for improving synthesis quality）。

为了在我们的学习系统中采用对抗性训练，我们添加了一个鉴别器D，用于区分解码器G生成的输出和实际的波形y。

在这项工作中，我们使用了两种成功应用于语音合成的损失类型：一种是对抗性训练的最小二乘损失函数，另一种是训练生成器的附加特征匹配损失。

T表示鉴别器中的层的总数，并且$D^{l}$输出具有$N_{l}$个特征的鉴别器的第l层的特征图。

值得注意的是，特征匹配损失可以被视为在鉴别器的隐藏层中测量的重建损失，该重建损失被建议作为VAE的逐元素重建损失的替代方案。

最终的损失函数

所有损失函数直接相加。

模型架构

总体架构由后验编码器、先验编码器、解码器、鉴别器和随机持续时间预测器组成。后验编码器和鉴别器仅用于训练，而不用于推理。

后验编码器

对于后验编码器，我们使用WaveGlow和Glow-TTS中使用的非因果WaveNet残差块, “the non-causal WaveNet residual blocks”。

WaveNet残差块由具有多个扩张卷积层（ dilated convolutions ），每层含有门控激活单元（gated activation unit）和跳跃连接（ skip connection）。块上方的线性投影层产生正态后验分布的均值和方差。

对于多个说话人的情况，我们在残差块中使用全局条件反射（global conditioning）来添加说话人embedding。

先验编码器

先验编码器包括处理输入音素$c_{text}$的文本编码器、改进先验分布的灵活性的归一化流 f 。

文本编码器是一种transformer编码器（transformer encoder），它使用相对位置表示（relative positional representation）而不是绝对位置编码（absolute positional encoding）。

我们可以通过文本编码器和文本编码器上方的线性投影层，从 $c{text}$ 中获得 hidden representation $h{text}$ ，该线性投影层产生用于构建先验分布的均值和方差。

归一化流(normalizing flow)是仿射耦合层（affine coupling layers）堆积而成，包含 WaveNet 残差块的堆栈。为了简单起见，我们将归一化流设计为雅可比行列式为1的保体积变换（a volume-preserving transformation with the Jacobian determinant of one）。

这个变换来自于 GLOW. https://arxiv.org/abs/1807.03039

对于多说话人设置，我们通过全局条件，将说话人embedding加入到归一化流中的残差块中。

解码器

解码器本质上是HiFi GAN V1生成器。它由”反条件姿态卷积”堆积组成，每个卷积后面，都有一个多接收场融合模块（MRF）。

MRF的输出是具有不同感受野大小的残差块的输出之和。

对于多说话人设置，我们添加一个转换说话人embedding的线性层，并将其添加到输入潜在变量z中。

判别器

我们遵循HiFi GAN中提出的多周期鉴别器的鉴别器架构。

多周期判别器是基于马尔可夫窗的子鉴别器的混合，每个子判别器对输入波形的不同周期模式进行操作。

随机持续时间预测器

随机持续时间预测器根据条件输入的 $h_{text}$ 估计音素持续时间的分布。

为了有效地参数化随机持续时间预测器，我们将残差块，与扩张和深度可分离的卷积层叠加。我们还将神经样条流（neural spline flows）应用于耦合层，其通过使用单调有理二次样条（monotonic rational-quadratic splines）采用可逆非线性变换的形式。

与常用的仿射耦合层相比，神经样条流的参数相似数量，但提高了变换的表现力。

对于多说话人设置，我们添加了一个线性层来转换说话人embedding，并将其添加到输入 $h_{text}$ 中。

个人理解

训练过程

使用了：

• 后验编码器
• 先验编码器
• 解码器
• 鉴别器
• 随机持续时间预测器

也就是所有部件。

$x_{lin}$ 为线性频谱, 通过后验编码器, flow, 解码器, 输出预测的原始波形 $\hat{y}$ .

$c{text}$ 为从文本中提取的音素, 通过文本编码器得到 $h{text}$ , 投影到 z 所服从的正态分布, 正态分布的两个参数是 $\mu{\theta}$ 和 $\sigma{\theta}$ . 然后使用单调对齐搜索( MAS )估计潜在变量之间的对齐 A ,最大化由归一化流 f 参数化的数据的可能性.

对齐 A 是一个硬单调注意力矩阵，其$\mid c{text}\mid \times \mid z\mid$维度, 表示每个输入音素$c{text}$扩展到与目标语音时间对齐的长度。

核心的 flow 是一堆 z 和一堆对应的 $fz(z)$ .对于 $\theta$ 层的 $z$, 服从的正态分布系数是 $\mu{\theta}$ 和 $\sigma_{\theta}$ ,

$f_{\theta}(z)$ ,

推理过程

使用了：

• 先验编码器
• 解码器
• 随机持续时间预测器

也就是不使用后验编码器和判别器。

$c_{text}$ ，phoneme（音素），作为输入。

经过text encoder，文本编码器，和线性投影层，得到 $h_{text}$ ，hidden representation，和投影。

$h_{text}$ 使用随机时间预测器，逆变换，从随机噪声中提取持续时间。

取样程序：通过随机持续时间预测器的逆变换，从随机噪声中采样音素持续时间，然后将其转换为整数，得到向量 $d$ 。

然后投入先验编码器，先验编码器包括文本编码器和归一化流，文本编码器是一个transformer，归一化流进行估计，参数化对先验概率q的逼近。

涉及的论文与概念

归一化流

本质是一个生成模型。一个基于可能性的生成模型。

（自回归模型, 生成对抗网络(GAN)的一部分, 变分自动编码器（VAE）也是自回归模型。）

Flow 将简单分布（易于采样和评估密度）映射到复杂分布（通过数据学习）。但是方便起见，实际使用时就是想办法得到一个encoder将输入x编码为隐变量z，并且使得z服从标准正态分布。

得益于flow模型的精巧设计，这个encoder是可逆的，从而我们可以立马从encoder写出相应的decoder（生成器）出来，因此，只要encoder训练完成，我们就能同时得到decoder，完成生成模型的构建。

---

x 和 z 应该有以下关系：

首先， $X=f(Z)$ ， $Z=f^{-1}(X)$ 。也就是说从 Z 映射到 X ，这个映射确定而可逆。

然后有：

变量变换定理(change of variable theorem): 有 $p_z(z)$ 和 $p_x(x)$ ,有 $f(z)=x$ ,如果要通过 $f$ 建立 $p_z(z)$ 和 $p_x(x)$ 之间的关系，可以将 $p_z(z)$ 和 $p_x(x)$ 使用微分方法借取一小段，直接计算一小段的体积，并对比，并按照体积的比例进行缩放，缩放函数在每个点上组合起来就是 $f(z)=x$ 。

$$p_x(x)=p_z(z) ( f^{-1}(x)) \mid {det}( \frac{\partial f^{-1}(x)}{\partial x} =p_z(z) ( f^{-1}(x)) \mid {det}( \frac{\partial f(x)}{\partial x}^{-1} ) \mid$$

其中，由于可逆矩阵 $det(A^{-1})=det(A)^{-1}$ 。因此对于 $z=f^{-1}(x)$ ，有：

$$p_x(x)=p_z(z) \mid {det}( \frac{\partial f(z)}{\partial z} ) \mid$$

对于 $\frac{\partial f^{-1}(x)}{\partial x}$ ，这是一个 n 维矩阵。这个矩阵记做雅可比矩阵。

保体积： $\mid {det}( \frac{\partial f(z)}{\partial z} ) \mid =1$ ，则从 z 到 x 的映射是保体积的。换言之，变换后的 $p_x$ 和 原始的 $p_z$ 有同样的体积，或者说volume。

(体积指的就是行列式.)

流模型核心条件：

• 模型可逆
• 对应的雅可比行列式容易计算
  • 因此本文将其设计为雅可比行列式为1的保体积变换（a volume-preserving transformation with the Jacobian determinant of one）

有“边界可能性” $p_x(x)$ ，满足

$$p_x(x;\theta )=p_z(f_{\theta }^{-1}(x)) \mid {det}( \frac{\partial f_{\theta }^{-1}(x)}{\partial x} ) \mid$$

名称“归一化流”可以解释如下：

• “归一化”意味着变量的变化在应用可逆变换后给出归一化密度（normalized density）。
• “流”意味着可逆变换可以相互组合，以创建更复杂的可逆变换。

存在多个隐变量 z, 存在对应数量的变换函数 f(z), 而最后一个 z 对应出来就是 x.

---

优化函数:

$$logp_k(x^i)=logp_z(z^i)+\sum_{h=1}^{K}log\mid det(J_{G^{-1}})\mid =logp_z(G^{-1}(x^i))+\sum_{h=1}^{K}log\mid det(J_{G^{-1}})\mid$$

这是 $G^{-1}$ 训练的目标: 最大化这个式子的值即可.

实际使用 G, 将其逆转即可.

平面流

vits使用的流模型

the non-causal WaveNet residual blocks used in WaveGlow (Prenger et al., 2019) and Glow-TTS (Kim et al., 2020).